How to write numbers in words?

1. Numbers in words in English

In this lesson, we will learn how to write numbers in words.

1- One

2- Two

3- Three

4- Four

5- Five

6- Six

7- Seven

8- Eight

9- Nine

10- Ten

11- Eleven

12- Twelve

13- Thirteen

14- Fourteen

15- Fifteen

16- Sixteen

17- Seventeen

18- Eighteen

19- Nineteen

20- Twenty

21- Twenty-one

22- Twenty-two

23- Twenty-three

24- Twenty-four

25- Twenty-five

26- Twenty-six

27- Twenty-seven

28- Twenty-eight

29- Twenty-nine

30- Thirty

31- Thirty-one

32- Thirty-two

33- Thirty-three

34- Thirty-four

35- Thirty-five

36- Thirty-six

37- Thirty-seven

38- Thirty-eight

39- Thirty-nine

40- Forty

41- Forty-one

42- Forty-two

43- Forty-three

44- Forty-four

45- Forty-five

46- Forty-six

47- Forty-seven

48- Forty-eight

49- Forty-nine

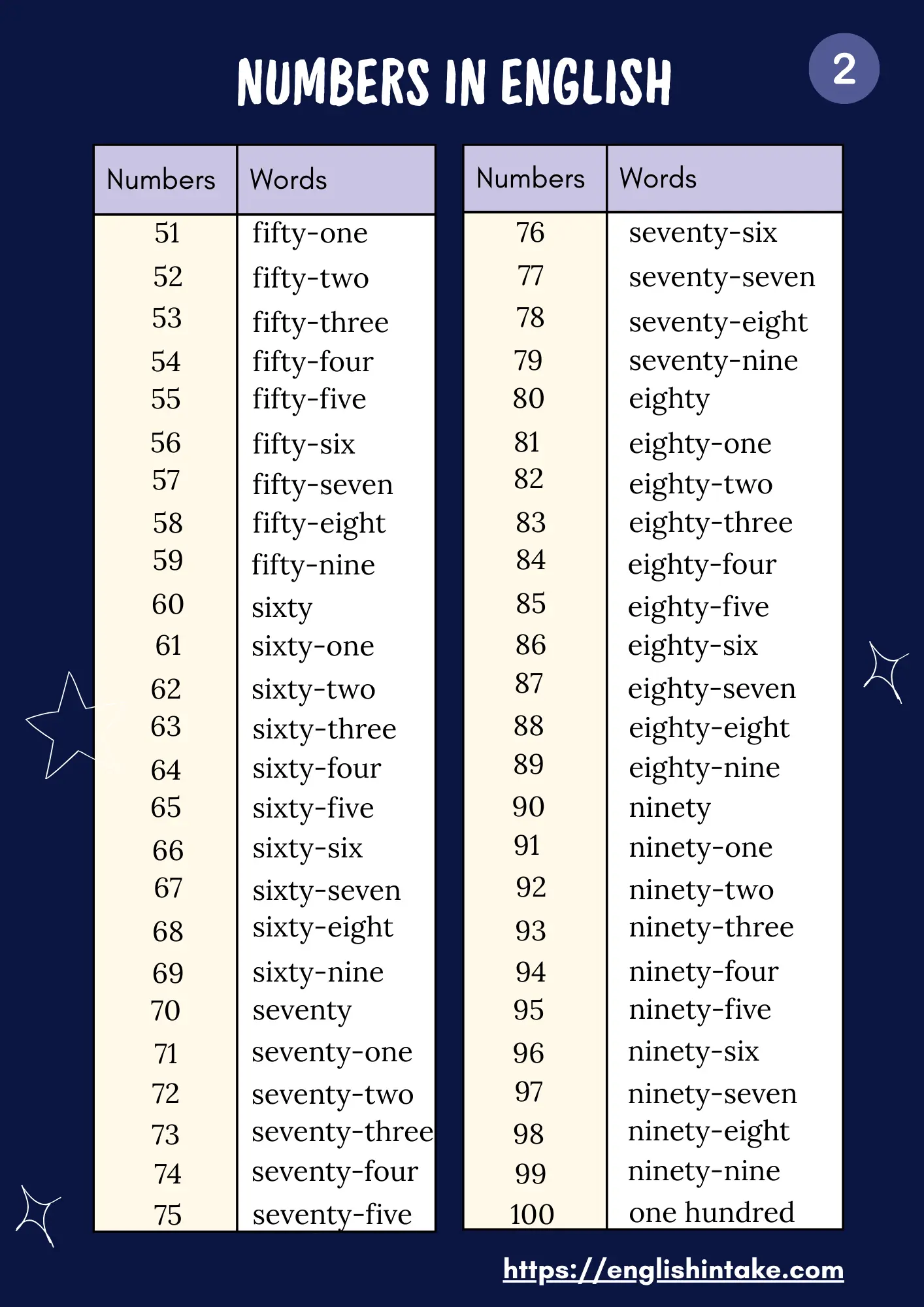
50- Fifty

51- Fifty-one

52- Fifty-two

53- Fifty-three

54- Fifty-four

55- Fifty-five

56- Fifty-six

57- Fifty-seven

58- Fifty-eight

59- Fifty-nine

60- Sixty

61- Sixty-one

62- Sixty-two

63- Sixty-three

64- Sixty-four

65- Sixty-five

66- Sixty-six

67- Sixty-seven

68- Sixty-eight

69- Sixty-nine

70- Seventy

71- Seventy-one

72- Seventy-two

73- Seventy-three

74- Seventy-four

75- Seventy-five

76- Seventy-six

77- Seventy-seven

78- Seventy-eight

79- Seventy-nine

80- Eighty

81- Eighty-one

82- Eighty-two

83- Eighty-three

84- Eighty-four

85- Eighty-five

86- Eighty-six

87- Eighty-seven

88- Eighty-eight

89- Eighty-nine

90- Ninety

91- Ninety-one

92- Ninety-two

93- Ninety-three

94- Ninety-four

95- Ninety-five

96- Ninety-six

97- Ninety-seven

98- Ninety-eight

99- Ninety-nine

100- One hundred

2. Types of numbers in English

Cardinal numbers

We use cardinal numbers to indicate quantity. They answer the question "How many?". Some examples include one, two, three, etc.

101- One hundred one

102- One hundred two

150- One hundred fifty

200- Two hundred

201- Two hundred one

204- Two hundred four

206- Two hundred six

250- Two hundred fifty

300- Three hundred

301- Three hundred one

305- Three hundred five

310- Three hundred ten

350- Three hundred fifty

400- Four hundred

410- Four hundred ten

425- Four hundred twenty-five

450- Four hundred fifty

500- Five hundred

600- Six hundred

700- Seven hundred

800- Eight hundred

900- Nine hundred

1,000- One thousand

2,000- Two thousand

5,000- Five thousand

10,000- Ten thousand

50,000- Fifty thousand

100,000- One hundred thousand

500,000- Five hundred thousand

1,000,000- One million

9,876,543 - Nine million, eight hundred and seventy-six thousand, five hundred and forty-three

For more practice, you can do our exercise on writing big numbers in English.

Ordinal numbers

We use ordinal numbers to indicate rank, order, or position.

1. Barack Obama was the first African-American president of the United States.

2. Donald Trump was the forty-fifth president of the United States.

3. My brother was awarded the second-best prize at Spain's annual International Festival of Music and Dance.

4. We live on the fourth floor.

1^st. first.

2^nd. second.

3^rd. third.

4^th. fourth.

5^th. fifth.

6^th. sixth.

7^th. seventh.

8^th. eighth.

9^th. ninth.

10^th. tenth.

11^th. eleventh.

12^th. twelfth.

13^th. thirteenth.

14^th. fourteenth.

15^th. fifteenth.

16^th. sixteenth.

17^th. seventeenth.

18^th. eighteenth.

19^th. nineteenth.

20^th. twentieth.

21^st. twenty-first.

22^nd. twenty-second.

23^rd. twenty-third.

24^th. twenty-fourth.

25^th. twenty-fifth.

26^th. twenty-sixth.

27^th. twenty-seventh.

28^th. twenty-eighth.

29^th. twenty-ninth.

30^th. thirtieth.

40^th. fortieth.

50^th. fiftieth.

60^th. sixtieth.

70^th. seventieth.

80^th. eightieth.

90^th. ninetieth.

100^th. hundredth.

101^st. hundred and first.

1000^th. thousandth.

100000^th. hundred thousandth.

1000000^th. millionth.

1000000000^th. billionth.

Fractional numbers

A fraction is a way to show the parts of a whole thing. Imagine you have a pizza. If you cut it into pieces and take just a few of those, you’re taking a fraction of the pizza. The quantity at the top (numerator) says how many pieces you have, and the bottom one (denominator) tells you how many pieces the whole pizza was cut into. So, if you have 2 pieces out of 8, you write it as 2/8.

1/2 - one over two (commonly known as half)

1/3 - one over three (one-third)

2/3 - two over three (two-thirds)

1/4 - one over four (a quarter or one-fourth)

3/4 - three out of four (three-quarters or three-fourths)

1/5 - one out of five (one-fifth)

2/5 - two out of five (two-fifths)

1/6 - one over six (one-sixth)

5/6 - five over six (five-sixths)

1/7 - one out of seven (one-seventh)

1/8 - one over eight (one-eighth)

1/10 - one out of ten (one-tenth)

7/10 - seven out of ten (seven-tenths)

1/20 - one over twenty (twentieth)

47/100 - forty-seven out of a hundred (forty-seven hundredths)

1/100 - one over a hundred (a hundredth)

1/1,000 - one over a thousand (a thousandth)

Decimal numbers

Reading rules:

1. Read the decimal point as "point.
2. Read decimal part individually.
3. Read the whole part normally.
4. Zeroes after the decimal point can be read as “zero” or “oh.”
5. 12.34 ”Twelve point three four“ ✘ Incorrect: “ Twelve point thirty-four. ”
6. 12.05 This can be read as “Twelve point zero five” or “Twelve point oh five.”

In certain contexts, like money, decimal numbers are read differently. For example, $3.50 might be read as “three dollars and fifty cents” instead of “three point five zero.”

3. Other types of numbers mostly used in mathematics

These include all whole numbers (both positive and negative) and zero: -3, -2, -1, 0, 1, 2, 3, etc.

They can be expressed as the quotient of two integers (a fraction) where the denominator is not zero: 1/2, -3/4, 5, 0.75, etc.

They cannot be expressed as a simple fraction; they have non-repeating, non-terminating decimal expansions: π (pi), √2 (the square root of 2), etc.

These include all rational and irrational numbers, including integers, and fractions 3.14, -1.5, 0, 2/3, etc.

Complex numbers include a real part and an imaginary part: a + bi (e.g., 4 + 5i), where bi is the imaginary part, and a is the real part.

Prime numbers are natural numbers greater than 1 that have no positive divisors other than 1 and themselves, including 2, 3, 5, 7, 11, etc.

These are natural numbers greater than 1 that are not prime; they have positive divisors other than 1 and themselves: 4, 6, 8, 9, 12, etc.

These are integers divisible by 2: -4, 0, 2, 6, etc.

These are integers not divisible by 2 like -3, 1, 5, 9, etc.